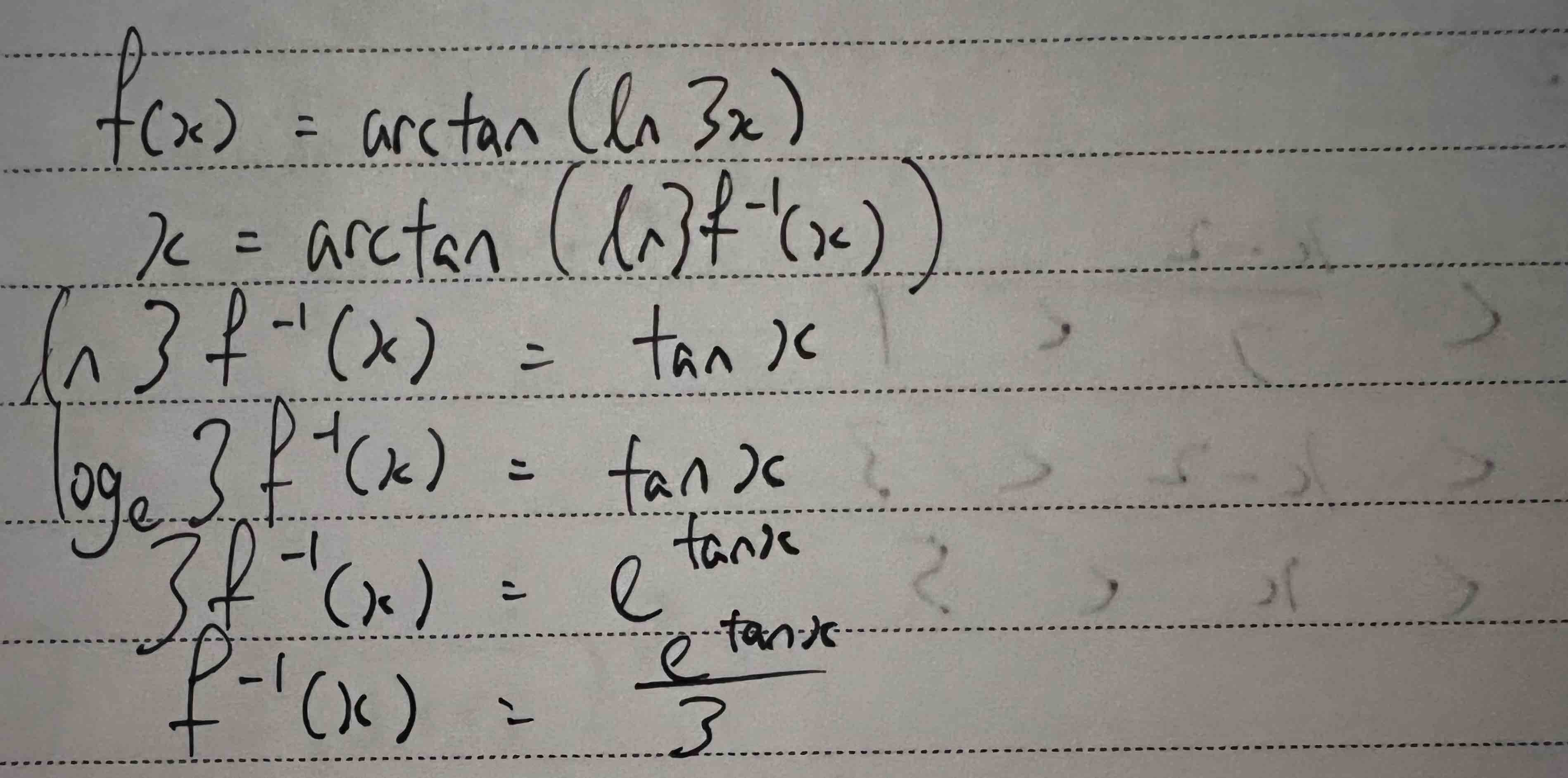Physx 3: Calculus Homework, Part 2

Continuing my series on calculus, I am doing the Practice Quiz on functions here.

Firstly, we need to understand the function of \(ln\) whose domain is \((0, +∞)\) and range \((-∞, +∞)\). That means we need to restrict \(\sin x\) to \((0, +∞)\), which is it’s range. i.e. What domain of \(\sin x\) would we have to restrict to produce a range of \((0, +∞)\)?

Taking a look at the domain & range of sin, we have this:

\begin{gather*} D = (-∞, +∞)\\ \Bbb R = (-1, 1) \end{gather*}

It is now clear that sine values between -1 and 0 inclusive is invalid. Hence, the answer is the domain of sine of which it produces values of range (0, 1). Recapping some common sine values, we can see that x can be between 0 and π. But not between π and 2π. This represents 1 oscillation of the sine wave. In the next oscillation, x is valid between 2π and 3π but invalid between 3π and 4π.

Hence, coming back to the question, n needs to be even to satisfy the above pattern. Back to the restriction we need with ln, 0 is not inclusive, so our range for x cannot include 0 as well. Therefore, the answer is the 3rd option: \(\big( n\pi, (n+1)\pi \big)\).

▬▬ι══════════════ι▬▬

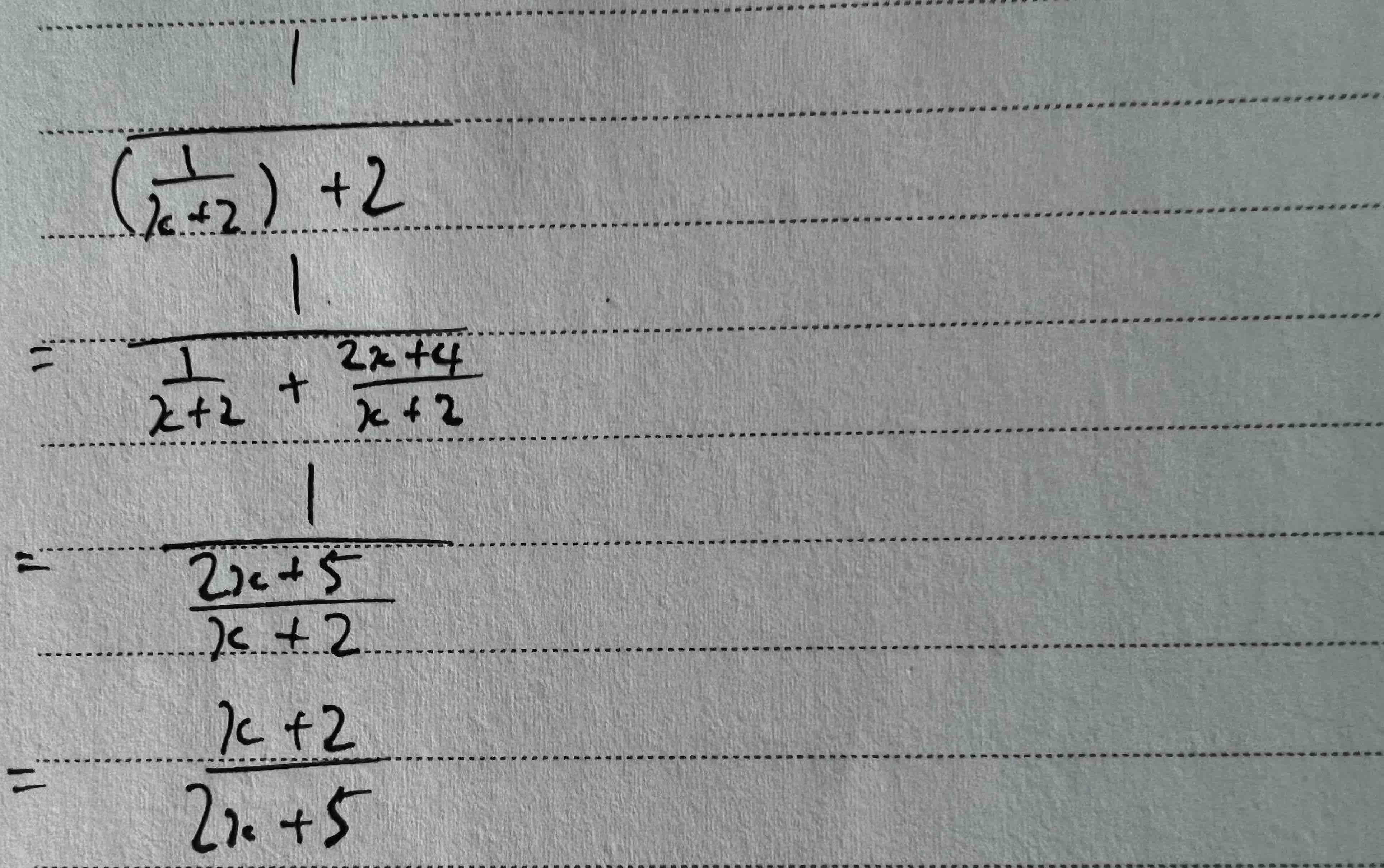
▬▬ι══════════════ι▬▬

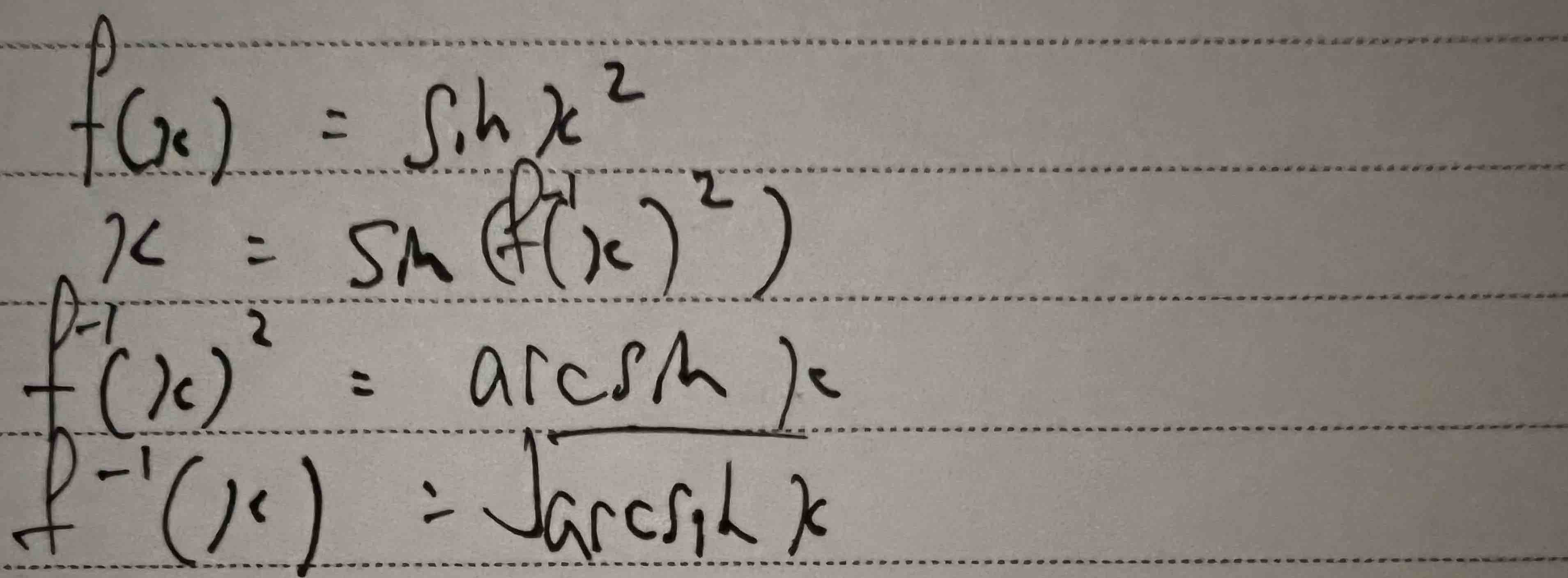
▬▬ι══════════════ι▬▬